Conditional Marginals
Published:
- Multivariate Copula Modeling
This R markdown is for Showcasing of continous non gaussian copula with conditional marginals
Table of content
Packages and setup
packages = c("brms","tidyverse","bayesplot",
"pracma","here", "patchwork",
"posterior","HDInterval",
"loo", "furrr","cmdstanr","mnormt")
do.call(pacman::p_load, as.list(packages))
knitr::opts_chunk$set(echo = TRUE)
register_knitr_engine(override = FALSE)
set.seed(11233)
Overview.
In this markdown the goal is to build on the previous markdown that showcased a gaussian copula with non-gaussian maginals. Here we now not only look at pure marginal continous distributions but at conditional continous distributions, as one would have in an experimental setting.
The setup
Lets say we again observe some VAS-ratings (VAS) bounded between 0 and 1 (not including the extremes to keep it simple) and response times (RT). Here we know that both response times and VAS ratings aren’t following a normal distribution as RT’s are positively skewed and non-negative and VAS ratings are bounded. Furthermore we will in this markdown assume that response time are getting slower and slower as trials progress, while VAS ratings gets lower.
Here we will simulate as in the previous markdown with three correlation coefficients, highly positive dependency ρ = 0.6, no dependency ρ = 0 and , no highly negative dependency ρ = −0.6. The main difference from the last markdown will be that for the marginals we will have:
The marginal distributions of the VAS a beta-distribution with μ = S−1(−2 + βc ⋅ Ti),ϕ = 20 again parameterized as mean and precision respectively with S−1(.) representing the inverse logit transform and Ti representing the trial number.
For the RT’s we assume a lognormal distribution with μ = −0.5 + βr**t * Ti and σ = 0.5.
For the simulations we will assume that βc and βr**t are -0.001 and 0.001 respectively
# Making the function to do the above:
get_responses = function(rho){
df = guassians = data.frame(mnormt::rmnorm(n = 100, mean = c(0,0),
varcov = cbind(c(1,rho),c(rho,1)))) %>% rename(VAS = X1, RT = X2)
uni_VAS = pnorm(df$VAS)
uni_RT = pnorm(df$RT)
betart = 0.01
betac = -0.01
VAS_mean = brms::inv_logit_scaled(1 + betac * 1:100)
RT_mean = -0.5 + betart * 1:100
VAS = extraDistr::qprop(uni_VAS,size = 20, mean = VAS_mean)
RT = qlnorm(uni_RT,RT_mean,0.5)
plot_pxy = data.frame(VAS = VAS, RT = RT) %>% ggplot() +
geom_point(aes(x = VAS,y = RT), size = 0.5)+
theme_minimal()+
ggtitle(paste0("p(VAS,RT) at rho = ",rho))+
theme(
plot.title = element_text(size = 20), # Increase title text size
axis.title = element_text(size = 16), # Increase axis titles text size
axis.text = element_text(size = 14) # Increase axis tick text size
)
plot_x = data.frame(VAS = VAS, RT = RT) %>% mutate(Trial = 1:n())%>%
ggplot() +
geom_point(aes(x = Trial, y = RT), size = 0.5)+
theme_minimal()+
ggtitle(paste0("p(VAS,RT) at rho = ",rho))+
theme(
plot.title = element_text(size = 20), # Increase title text size
axis.title = element_text(size = 16), # Increase axis titles text size
axis.text = element_text(size = 14) # Increase axis tick text size
)
plot_y = data.frame(VAS = VAS, RT = RT) %>% mutate(Trial = 1:n())%>%
ggplot() +
geom_point(aes(x = Trial, y = VAS), size = 0.5)+
theme_minimal()+
ggtitle(paste0("p(VAS,RT) at rho = ",rho))+
theme(
plot.title = element_text(size = 14), # Increase title text size
axis.title = element_text(size = 10), # Increase axis titles text size
axis.text = element_text(size = 10) # Increase axis tick text size
)
plot = plot_pxy / plot_x / plot_y
return(list(plot = plot, data = data.frame(VAS = VAS, RT = RT, cor = rho)))
}
Plotting the results of using the function at the level of the response variables (i.e. Ratings and response times)
get_responses(-0.6)[[1]]|get_responses(0)[[1]]|get_responses(0.6)[[1]]
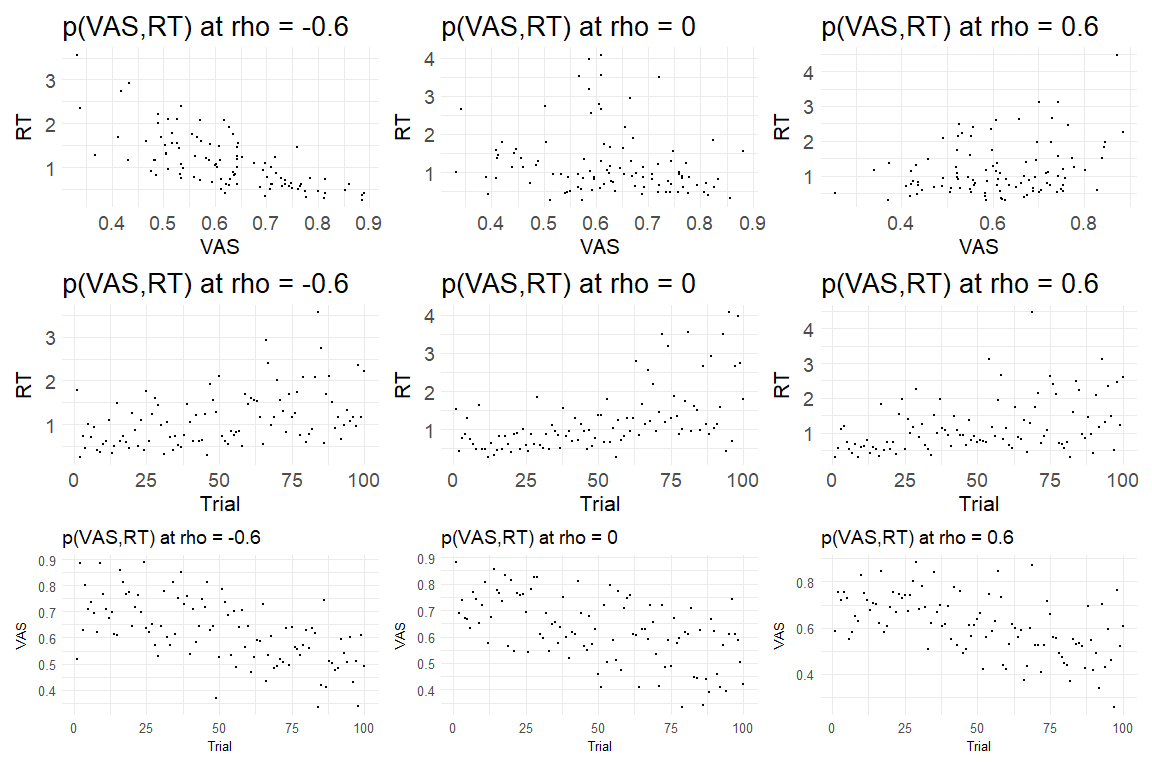
Now we have data that kind of looks like something from an experiment the question is can we recover the parameters we put in? In order to do this we write the stan model:
functions {
real gauss_copula_cholesky_lpdf(matrix u, matrix L) {
array[rows(u)] row_vector[cols(u)] q;
for (n in 1:rows(u)) {
q[n] = inv_Phi(u[n]);
}
return multi_normal_cholesky_lpdf(q | rep_row_vector(0, cols(L)), L)
- std_normal_lpdf(to_vector(to_matrix(q)));
}
}
data {
int<lower=0> N;
matrix[N, 2] Y;
}
parameters {
real mu_beta;
real<lower=0> prec_beta;
real mu;
real<lower=0> sigma;
real betart;
real betac;
cholesky_factor_corr[2] rho_chol;
}
model {
matrix[N, 2] u;
for (n in 1:N) {
u[n, 1] = exp(beta_proportion_lcdf(Y[n, 1] | inv_logit(mu_beta + betac * n),prec_beta));
u[n, 2] = lognormal_cdf(Y[n, 2] | mu + betart * n,sigma);
Y[n, 1] ~ beta_proportion(inv_logit(mu_beta + betac * n),prec_beta);
Y[n, 2] ~ lognormal(mu + betart * n,sigma);
}
u ~ gauss_copula_cholesky(rho_chol);
mu_beta ~ normal(0,1);
prec_beta ~ normal(10,10);
mu ~ normal(0,3);
sigma ~ normal(0,3);
betart ~ normal(0,0.5);
betac ~ normal(0,0.5);
rho_chol ~ lkj_corr_cholesky(2); // LKJ prior on correlation matrix
}
generated quantities {
real rho = multiply_lower_tri_self_transpose(rho_chol)[1, 2];
}
Displaying if we can recover!
parameters = c("mu_beta","prec_beta","mu","sigma","rho", "betart","betac")
data = rbind(data.frame(fit_corm08$summary(parameters)) %>% mutate(simulated = c(1,20,-0.5,0.5,-0.6,0.01,-0.01), sim_cor = -0.8),
data.frame(fit_cor0$summary(parameters)) %>% mutate(simulated = c(1,20,-0.5,0.5,0,0.01,-0.01), sim_cor = 0),
data.frame(fit_cor08$summary(parameters)) %>% mutate(simulated = c(1,20,-0.5,0.5,0.6,0.01,-0.01), sim_cor = 0.8))
data %>% mutate(sim_cor = as.factor(sim_cor)) %>%
ggplot(aes(x = simulated, y = mean, ymin = q5, ymax = q95, col = sim_cor))+
geom_pointrange(position=position_dodge(width=0.01))+
facet_wrap(~variable,scales = "free", nrow = 1)+
theme_minimal(base_size = 16)+
geom_hline(aes(yintercept = simulated), data = data,
color = "grey70", linetype = "dashed")+
scale_x_continuous(breaks = scales::pretty_breaks(n = 3))
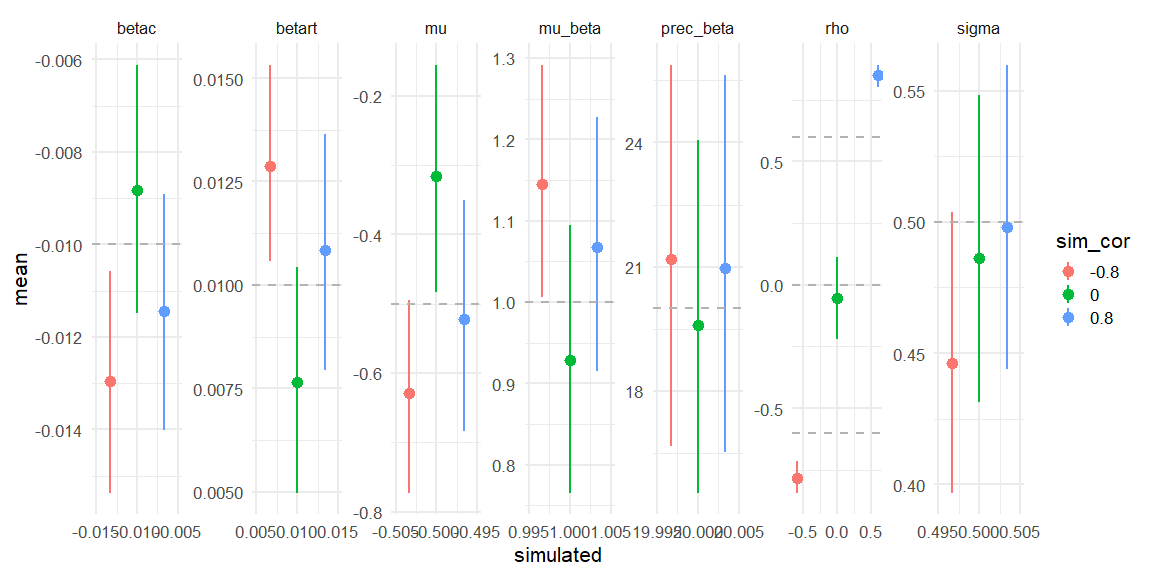
Here we see that all three models do recover the simulated parameters (inside the 90% HDI) (values depicted as the grey line).
Further exploration
One might give two objections or point of further investigation.
The Second objection is that for now this has only been done for continuous probability distributions. In order for this to be versatile we need to show that we can do the same for discrete probability distributions such as possion and binominal random variables.
The Third is that these these implementations are purely in a single subject framework and needs to be tested hierarchically, I.e. estimation subject level parameters nested within a group.
These steps are implemented in the next 3-markdowns!
